L’activité proposée ici reprend l’idée d’une modélisation de la dérive génétique par tirage de billes de couleurs (voir l’article correspondant), en la simplifiant et en l’utilisant également pour la sélection naturelle, le tout étant réalisable au sein d’une même séance de TP.
La démarche est expliquée de manière détaillée en justifiant les choix réalisés. Différents documents en fin d’article récapitulent les protocoles et peuvent servir de support à la réalisation de fiches d’activité pour les élèves.
Sommaire :
Prérequis
Partie couverte du programme
Matériel nécessaire
Explication de la démarche
Activité 1 : Modélisation de la dérive génétique
Activité 2 : Influence de l’effectif sur la dérive génétique
Activité 3 : Modélisation de la sélection naturelle
Documents complémentaires
Prérequis :
– Le terme de biodiversité est utilisé pour désigner la diversité du vivant et sa dynamique aux différentes échelles, depuis les variations entre membres d’une même espèce (diversité génétique) jusqu’aux différentes espèces et aux écosystèmes composant la biosphère.
– Au sein de chaque espèce, la diversité des individus repose sur la variabilité de l’ADN : c’est la diversité génétique. Différents allèles d’un même gène coexistent dans une même population, ils sont issus de mutations qui se sont produites au cours des générations.
Partie couverte du programme :
Thème 1 : La Terre, la vie et l’organisation du vivant
| La dérive génétique est une modification aléatoire de la fréquence des allèles au sein d’une population au cours des générations successives. Elle se produit de façon plus rapide lorsque l’effectif de la population est faible. La sélection naturelle résulte de la pression du milieu et des interactions entre les organismes. Elle conduit au fait que certains individus auront une descendance plus nombreuse que d’autres dans certaines conditions. |
- Utiliser un logiciel de modélisation et/ou extraire et mettre en relation des informations pour illustrer la sélection naturelle et la dérive génétique sur des temps courts. - Réfléchir sur les conséquences de l’apparition aléatoire de mutants sur la dynamique d’une population. |
Matériel nécessaire :
Pour chaque binôme, prévoir :
– Une boîte opaque avec couvercle ou un grand sac noir
– Une petite boîte (style boîte de Pétri), en plastique
– Billes ou boules de 3 couleurs différentes (environ 15 boules de chaque couleur), mais de même taille et de même texture (exemple : boules de cotillon, 1 sachet de 1000 boules suffit pour une classe).
Tous les groupes doivent avoir le même nombre de boules au départ. Le nombre de boules doit être identique pour chaque couleur. Pour faciliter la mise en commun des résultats, il est préférable que les 3 couleurs doivent être les mêmes pour tous les groupes.
Eventuellement au bureau, prévoir une réserve de boules de couleurs supplémentaires.
Explication de la démarche
On peut introduire les activités en commençant par rappeler que l’on sait que tous les êtres vivants sont plus ou moins apparentés, ils partagent un ancêtre commun.
– On cherche à comprendre par quel(s) mécanisme(s) les espèces ont évolué au cours du temps.
Arrivé à ce point du programme, il peut y avoir en effet une sorte de paradoxe entre les preuves qui montrent que tous les êtres vivants sont apparentés et l’extraordinaire richesse que présentent les êtres vivants actuels et passés. Certes, dans une famille, tous les individus sont apparentés, mais il est en général assez facile de les reconnaître... Cela n’est pas le cas pour tous les êtres vivants à première vue.
Evidemment, l’explication à la fin de la séance est qu’au cours des temps géologiques, l’évolution fait son œuvre. Mais cela implique de prendre du recul : si à l’échelle de temps humaine l’évolution n’est quasiment pas perceptible, ce n’est pas le cas sur les millions et les milliards d’années de l’histoire de la vie sur Terre.
Ce TP peut également être l’occasion de se rendre compte d’explications finalistes que peuvent avoir certains ("Les poissons sont faits pour nager. / Les animaux sont sortis de l’eau pour marcher sur la terre ferme. / S’il y a des bousiers, c’est qu’il y en a besoin, qu’ils sont indispensables. / Le paon mâle a une queue colorée pour plaire aux femelles. / Les girafes ont un grand cou pour brouter les feuilles des arbres..."). Ce sont d’une certaine façon des explications argumentées de la biodiversité actuelle et qui peuvent sembler logiques. Mais le problème est qu’on cherche alors à donner un sens, une volonté à la nature et que ces arguments dépendent du point de vue où l’on se place. Il ne s’agit donc pas d’arguments scientifiques.
Dérive génétique et sélection naturelle permettent une explication plus rationnelle et universelle, caractéristiques que ne possèdent pas les raisonnements finalistes.
On arrivera en quelque sorte à la conclusion de Theodosius Dobzhansky : « Rien n’a de sens en biologie, si ce n’est à la lumière de l’évolution. »
- Pourquoi une activité de modélisation ?
Les occasions dans le programme ne sont pas toujours très fréquentes. Autant s’en donner l’occasion, surtout lorsque cela peut être fait de manière simple. Ici, les élèves sont amenés à utiliser un modèle qui leur est fourni, mais rien n’empêche de leur faire trouver une idée de modélisation, ou bien : une fois faite la modélisation de la dérive génétique, leur demander d’adapter le modèle à la sélection naturelle (après explication du concept, bien sûr).
Il existe des logiciels permettant de manipuler un modèle comparable à ce qui est proposé ici, ou de concevoir et réaliser une modélisation de A à Z, mais ils nécessitent une prise en main et surtout, cela ne rend pas vraiment concret la modélisation. D’autre part, on ne peut pas forcément les adapter au cas de la sélection naturelle. Ceci dit, ils peuvent aussi être complémentaires ou remplacer une partie de ces activités.
- Un modèle est à utiliser avec précaution
Les élèves doivent comprendre que le modèle n’est pas choisi au hasard, que l’on a choisi de symboliser un phénomène, donc d’essayer de le reproduire en le simplifiant, pour le comprendre. C’est donc une approche, discutable, d’un phénomène.
- Savoir mettre en évidence les limites du modèle
C’est l’occasion d’exercer son esprit critique. Pourquoi fait-on comme ceci et pas autrement ? Comment pourrait-on améliorer le modèle ?...
Activité 1 : Modélisation de la dérive génétique (environ 30 min)
- Mise au point préliminaire : Qu’est-ce que la dérive génétique ?
Selon le programme, la dérive génétique est une modification aléatoire de la fréquence des allèles au sein d’une population au cours des générations successives. Elle se produit de façon plus rapide lorsque l’effectif de la population est faible.
Autrement dit, si on prend au départ une population constituée de différents lignages possédant une fécondité identique des individus, on va aboutir, après plusieurs générations, à une population différente de la population de départ : une population dont les fréquences des allèles et donc des caractères héréditaires se sont modifiées.
En effet, au cours des aléas de la vie, chaque lignage laisse plus ou moins de descendants, ce qui modifie les proportions d’individus de chaque lignage à chaque génération. Il y a donc modification de la biodiversité au cours du temps.
On ne prend donc pas en compte ici la possibilité de mutations ou une pression sélective : chaque lignage de départ a autant de probabilité que les autres de donner des descendants.
Le rôle des mutations comme cause de variation génétique seront abordés après cette 1ère modélisation.
- Comment peut-on modéliser la dérive génétique ?
Le modèle doit respecter certains principes (contraintes) :
- Partir d’une population avec une certaine biodiversité, donc composée de différents lignages, appartenant tous à la même espèce
- Chaque lignage possède la même probabilité de se reproduire que les autres
- Le nombre de descendants est dû aux aléas de la vie : il est dû au hasard (cette information doit être déduite par les élèves après utilisation du modèle).
On va donc suivre l’évolution au cours des générations, de la fréquence de chaque lignage d’une population, dont les individus ont un nombre aléatoire de descendants.
D’où les choix réalisés :
- On utilise des billes ou des boules (ou autre...), représentant des individus différents.
- On détermine le nombre de couleurs différentes dans la population de départ, autrement dit le nombre de lignages différents.
- Chaque lignage possède le même nombre de représentants au départ, il y a donc autant de billes de chaque couleur au départ.
- En fonction des aléas de la vie, certains individus se reproduisent, d’autres pas. On va donc piocher sans regarder dans la population de départ les individus qui vont se reproduire.
- Le nombre de descendant de chaque individu est dû au hasard, d’où l’utilisation d’un dé : le lancer de dé indique le nombre de descendants. A moins d’avoir des dés pipés, il y aura donc une équiprobabilité d’avoir de 1 à 6 descendants...
- Les descendants obtenus (= enfants) constituent la nouvelle génération. On peut par exemple compter le nombre de billes de chaque couleur pour comparer les proportions avec la génération précédente. Il suffit de continuer le jeu en repiochant parmi cette nouvelle génération les individus qui vont se reproduire, de relancer le dé pour connaître le nombre de leurs descendants et donc de constituer la génération n+1, etc.
La simulation s’arrête lorsque toutes les boules sont de la même couleur, ou par exemple à la 7e génération maximum.
Pour obtenir des résultats plus statistiques, il faut recommencer plusieurs simulations et comparer les résultats.
Voici le protocole proposé :
| Départ |
|---|
Chaque groupe d’élève possède un stock de boules de 3 couleurs différentes (de même proportions), un dé et une autre boîte, vide.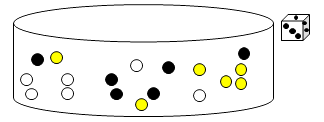
|
| Règles du jeu - Dérive génétique |
|---|
| Etape 1 : Un élève de chaque groupe effectue un tirage au sort de 3 boules de la grande boîte (cela doit impérativement se faire au hasard) et les pose sur le couvercle. 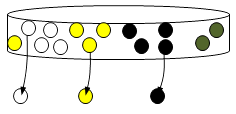
|
| Etape 2 : Pour chaque boule piochée, lancer le dé. Le chiffre obtenu indique combien de boules de cette couleur il faut mettre dans la boîte de Petri. 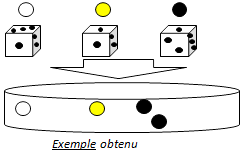
|
| Etape 3 : Vous avez obtenu une génération dans votre boîte de Pétri. Noter dans un tableau le résultat obtenu. C’est à partir de cette nouvelle génération que des individus vont se reproduire. Vous pouvez ranger toutes les boules qui vous restent, sauf celles de votre nouvelle génération. Il faut donc recommencer les étapes 1 et 2, mais en piochant sans regarder à nouveau 3 boules dans la boîte de Pétri,... L’activité s’arrête lorsqu’il ne reste que des boules d’une seule couleur ou lorsque la 7e génération est atteinte. |
Exemple de résultat :
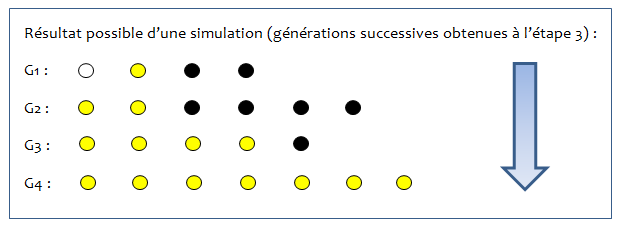
Protocoles téléchargeables, avec signification de chaque étape, pour la modélisation de la dérive génétique :
| Version .doc | Version PDF |
|---|---|
Attention, les couleurs de boules différentes peuvent correspondre soit à un caractère héréditaire observable, soit à l’un des allèles d’un gène (toutes les couleurs ne sont alors que les allèles d’un même gène). Cela ne change rien aux règles du jeu proposées. C’est plus logique de parler d’allèles puisqu’on travaille sur la dérive génétique, mais cette simple modélisation ne permet pas de prendre en compte les 2 allèles d’un même gène (= chez les diploïdes), alors que cela marche si l’on se place chez des haploïdes.
D’ailleurs, on pioche plusieurs individus dans la population de départ et pour chaque individu pioché, on va lancer le dé pour savoir combien de descendants il va engendrer. Dans le modèle présenté ici, chaque individu se reproduit donc seul. Ce n’est pas impossible dans la réalité puisque cela correspondrait à de la reproduction asexuée. Du coup, en considérant les individus comme haploïdes, on a automatiquement la correspondance entre l’allèle possédé et le caractère exprimé. Cela lève l’ambigüité de la signification de la couleur dans ce modèle.
La modélisation proposée est une première approche. C’est normal qu’elle ne puisse pas prendre tout en compte. Mais ce qui est important, c’est que cela ne change ni le mécanisme étudié ni les résultats : ce que l’on va observer est transposable chez les diploïdes.
Il n’est donc pas indispensable d’évoquer les termes diploïdes / haploïdes avec les élèves. Il suffit de présenter la modélisation en expliquant qu’il s’agit là d’une première approche et que l’on a simplifié par rapport à la réalité, sans avoir de conséquence sur le phénomène étudié et que ce mode de reproduction, même s’il n’est pas le plus courant, existe quand même dans la nature.
- Exemple de déroulement de l’activité 1
– Après introduction et présentation de la problématique, explication du principe de la modélisation : on cherche à simuler l’évolution de la diversité allélique d’une population au cours des générations.
– Explication du modèle utilisé, de la signification du matériel choisi.
– Présentation et lancement des simulations (distribution des "règles du jeu", du protocole).
– Au bout de 20 minutes par exemple, on arrête les simulations. On met en commun les impressions des élèves, les observations. On soulignera notamment les proportions des différentes couleurs obtenues à la fin de chaque simulation, les résultats souvent différents à chaque génération et à chaque fin de simulation. On remarque qu’une couleur finit souvent par l’emporter sur les autres, plus ou moins rapidement, mais qu’en recommençant les simulations, ce n’est pas toujours la même.
C’est l’occasion de réfléchir sur ce que représentent les boules de couleur et le mécanisme à l’origine de cette variation : à partir d’une même proportion de phénotypes dans la population de départ, on a pioché sans regarder et utilisé le dé. Tout a l’air une question d’aléatoire, de hasard. D’où la notion de dérive génétique...
- Détails pratiques
– Combien de lignages (couleurs) différents utiliser au total ?
Théoriquement, autant que vous voulez. Sur un paquet de 1000 boules de cotillon, après triage des boules, j’ai eu par exemple tout juste de quoi faire pour chaque groupe de TP 6 couleurs différentes avec 10 boules à chaque fois. Le matériel est évidemment réutilisable.
Mais finalement, j’ai choisi de ne prendre que 3 couleurs différentes, tout d’abord pour simplifier la procédure et la mise en commun. Mais surtout parce que j’ai voulu modéliser le cas du gène du groupe sanguin : 1 gène, 3 allèles différents. Chaque couleur choisie correspond donc à un allèle concret, ce qui contribue à rendre le modèle plus réaliste.
– Combien prévoir de boules de chaque couleur pour chaque binôme de TP ?
Théoriquement, il suffit de compter le maximum de boules nécessaires. Si on pioche au hasard 3 boules à chaque génération et qu’on obtient le score maximal de 6 au dé à chaque fois, il y a besoin théoriquement de 18 boules de chaque couleur. Dans la pratique, 12 à 15 boules sont suffisantes.
– Combien piocher de boules à chaque génération ?
Les boules piochées au hasard dans la population d’une génération correspondent aux géniteurs, à ceux qui se reproduisent et auront des descendants. Ce choix n’est pas anodin, puisqu’il faudra montrer par la suite que la dérive génétique se produit de façon plus rapide lorsque l’effectif de la population est faible.
J’ai choisi de commencer avec 3 géniteurs à piocher au hasard. Plus ce nombre est important, plus il faut prévoir de boules pour chaque binôme et plus le temps passé pour chaque simulation sera important...
– Où mettre les boules au cours du jeu ?
Une gestion rigoureuse du matériel est indispensable, de même qu’un suivi identique du protocole par tous les groupes, sinon les résultats ne seront pas comparables.
Le grand sac ou la grande boite contiendront la population initiale, puis le stock de boules restantes lors de chaque simulation.
Lorsque l’on pioche au hasard, on isole les géniteurs par exemple sur une feuille ou sur le couvercle de la grande boîte.
Pour chaque géniteur, on lance le dé ; on place alors dans la boite de Pétri le nombre exact de boules de couleur correspondantes, que l’on aura pris dans le stock. La boîte de Pétri contient donc la nouvelle génération.
On replace les géniteurs dans le stock de boules : on choisit de ne pas les mettre dans la nouvelle génération (le fait de choisir le contraire ne change pas les résultats, mais dans un cas comme dans l’autre, il faut que tous les élèves fassent pareil).
On pioche les nouveaux géniteurs parmi la nouvelle génération, donc dans la boîte de Pétri. Ils seront à nouveau isolés sur une feuille le temps de la phase des dés. Pendant ce temps, les boules restantes de l’ancienne génération reviennent dans le stock : on choisit de ne pas les cumuler à la nouvelle génération (on aurait très bien pu faire le contraire bien sûr, mais il faut prévoir plus de boules de chaque couleur au départ). Et ainsi de suite...
Activité 2 : La dérive génétique se produit de façon plus rapide lorsque l’effectif de la population est faible (durée au choix)
Il y a plusieurs façons possibles d’aborder ce point sans rentrer dans les détails.
– 1ère possibilité :
Lors de la discussion à la fin de l’activité 1, certains élèves ont pu se rendre compte que moins une génération comporte d’individus, plus la génération suivante peut différer de la génération précédente. A condition bien sûr de comparer des générations aux proportions équivalentes de couleurs différentes.
– 2e possibilité :
Introduction d’un document complémentaire montrant par exemple les résultats d’une autre simulation, où on a fait varier l’effectif de la population. En voici un exemple :
| Version .doc | Version PDF |
|---|---|
– 3e possibilité :
Recommencer l’activité 1 en faisant varier le nombre de géniteurs. Dans ce cas, il faudra avoir prévu beaucoup plus de boules ou billes de chaque couleur, surtout si l’on veut que le phénomène soit bien visible. Autre inconvénient : cela nécessite sans doute plus de temps que les 2 premières possibilités.
– 4e possibilité :
Utilisation d’un logiciel de simulation permettant de faire varier l’effectif de la population. Exemples : Modélisation de la dérive génétique par tirages successifs avec remise, Modélisation de l’évolution de la fréquence allélique
(dérive génétique), ou : netBioDyn (voir cet article pour des explications complémentaires).
Moins chronophage que la 3e possibilité et avec modélisation de l’effet des mutations (logiciel Modélisation de la dérive génétique par tirages successifs avec remise).
Activité 3 : Modélisation de la sélection naturelle (environ 15 min)
- Mise au point préliminaire : Qu’est-ce que la sélection naturelle ?
Certains allèles procurent à ceux qui les portent un avantage ou un désavantage pour la survie et la reproduction. Ces allèles sont donc plus ou moins transmis de génération en génération, en fonction des conditions du milieu. C’est la sélection naturelle.
L’environnement est constitué de multiples facteurs qui opèrent une sélection naturelle à chaque génération. Elle correspond donc à un succès reproductif différentiel, qui ne peut s’observer qu’à l’échelle d’une population.
- Comment peut-on modéliser la sélection naturelle ?
Le modèle doit respecter les contraintes suivantes :
- Partir d’une population avec différents lignages, mais appartenant tous à la même espèce.
- Les lignages possèdent des probabilités différentes de se reproduire : certains se reproduisent mieux que d’autres.
On suit toujours l’évolution au cours des générations, de la fréquence de chaque lignage d’une population. On reprend donc les mêmes règles du jeu que pour la dérive génétique. Il suffit de rajouter une étape supplémentaire : on choisit la couleur de bille qui devient favorable ; les billes de cette couleur auront par exemple 2 fois plus de descendants que les autres. Le protocole est donc le même ; on ne change qu’un facteur.
Chaque groupe d’élève peut choisir sa couleur préférée et la conserve au cours des simulations. Il s’agit donc d’un choix arbitraire qui montre que la sélection naturelle dépend des conditions environnementales : un même caractère peut se retrouver favorable, défavorable ou neutre selon les conditions.
Voici le protocole possible pour la modélisation de la sélection naturelle :
| Départ |
|---|
Chaque groupe d’élève possède un stock de boules de 3 couleurs différentes (de même proportions), un dé et une autre boîte, vide.
|
| Règles du jeu - Sélection naturelle |
|---|
| Différence par rapport à la modélisation de la dérive génétique : On considère qu’un caractère est bénéfique pour ceux qui les portent : ils se reproduisent 2 fois plus. Choisir et noter ce caractère parmi les 3 couleurs possibles : (conserver ce choix pour tous vos essais) - A l’étape 2, pour chaque boule piochée correspondant à ce caractère bénéfique, on multipliera par 2 le chiffre obtenu au dé. |
| Etape 1 : Un élève de chaque groupe effectue un tirage au sort de 3 boules de la grande boîte (cela doit impérativement se faire sans regarder) et les pose sur le couvercle. 
|
| Etape 2 : Pour chaque boule piochée, lancer le dé. Le chiffre obtenu indique combien de boules de cette couleur il faut mettre dans la boîte de Petri. 
|
| Etape 3 : Vous avez obtenu une génération dans votre boîte de Pétri. Noter dans un tableau le résultat obtenu. C’est à partir de cette nouvelle génération que des individus vont se reproduire. Vous pouvez ranger toutes les boules qui vous restent, sauf celles de votre nouvelle génération. Il faut donc recommencer les étapes 1 et 2, mais en piochant au hasard à nouveau 3 boules dans la boîte de Pétri,... L’activité s’arrête lorsqu’il ne reste que des boules d’une seule couleur ou lorsque la 7e génération est atteinte. |
Protocoles téléchargeables, avec signification de chaque étape, pour la modélisation de la sélection naturelle :
| Version .doc | Version PDF |
|---|---|
- Exemple de déroulement de l’activité 2
– Présentation de la sélection naturelle et réflexion sur la manière dont on peut modifier le protocole pour y arriver.
– Explication de la nouvelle étape et lancement des simulations.
– Arrêt au bout de 10-15 minutes et mise en commun des résultats. On remarque que parfois, la couleur choisie arrive à l’emporter sur les autres, mais pas toujours (effet cumulé de la dérive génétique et de la sélection naturelle). Il suffit de compter le nombre de binômes où la couleur favorite est arrivée à la fin des simulations pour se rendre compte que la probabilité est très importante (j’ai obtenu entre 75 et 100% selon les classes). D’où la notion de sélection naturelle...
Conclusion
La combinaison dérive génétique + sélection naturelle permet d’expliquer de manière rationnelle une certaine variation de la biodiversité au cours du temps. La biodiversité n’est donc pas figée, même naturellement. On n’atteint pas un état "optimal" d’adaptation. Il n’y a pas de progression vers une sorte de but : la biodiversité actuelle est le fruit de l’évolution passée des êtres vivants, en interaction avec leur environnement, ce qui justifie d’ailleurs d’avoir traité dans une même partie l’évolution de la vie et la planète Terre.
Poursuite
Dans le monde animal, la communication interindividuelle et les comportements induits peuvent contribuer à la sélection naturelle à travers la reproduction. C’est le cas pour la sélection sexuelle entre partenaires (majoritairement faite par les femelles).
Documents complémentaires
– Schéma-bilan : Rôles de la dérive génétique et de la sélection naturelle dans la variation de la biodiversité
| Version .doc | Version PDF |
|---|---|
(Schéma adapté de la Banque de schémas - SVT)
– Un exemple de sélection naturelle : l’évolution du VIH chez un patient
(voir la figure 4 et son explication).
Voir aussi :
– La dérive génétique dans le cadre du programme de Seconde
– Evolution de la biodiversité des allèles : A, B, O






