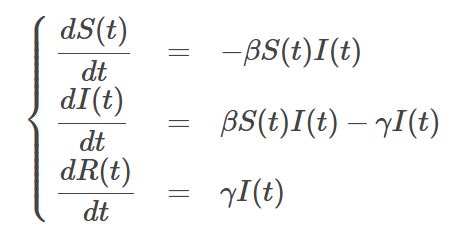Première spécialité SVT

Un modèle à compartiment pour les épidémies : le modèle SIR

avec l’outil Édu’modèles (P. Cosentino)

Les modélisations occupent une place importante dans les sciences actuelles, ce qui justifie l’intérêt qui leur est porté dans les derniers programmes. De nombreuses propositions d’activités de modélisation ont été publiées sur les sites académiques, s’appuyant sur les logiciels NetBioDyn ou Édu’modèles. La majorité de ces propositions exploitent des modèles multi-agents où sont définies des entités individuelles dont on paramètre les propriétés et les comportements.
On propose ici de faire connaître aux élèves de Première Spécialité une autre famille de modèles qui auront leur importance en Terminale : les modèles à compartiments.

ressources immunologie modélisation 1ère_Spécialité_Le fonctionnement du système immunitaire humain GEP

Mis à jour le mardi 27 juin 2023 , par Bruno Boucher

Professeur

Bruno BOUCHER, au lycée Camille Claudel, Vauréal (95)

Caractéristiques de la séquence

LIAISON AVEC LE PROGRAMME
Niveau concerné	Première Spécialité
Partie du programme	Thème Corps humain et santé - Le fonctionnement du système immunitaire humain

PLACE DANS LA PROGRESSION
L’activité proposée intervient en fin de thème. Les mécanismes de l’immunité ont été explicités et le principe de la vaccination a été posé. Le modèle à compartiment a été introduit après avoir utilisé le modèle multi-agents proposé par Anne Florimond dans cet article afin de valider l’intérêt de la vaccination d’un point de vue collectif et pas seulement individuel.

MOTIVATION
Les modèles à compartiments sont utiles dans différents champs scientifiques, et sont des classiques de l’épidémiologie. Il peut donc apparaître pertinent de les faire connaître aux élèves, en complément des modèles multi-agents.

PROBLÈME À RÉSOUDRE
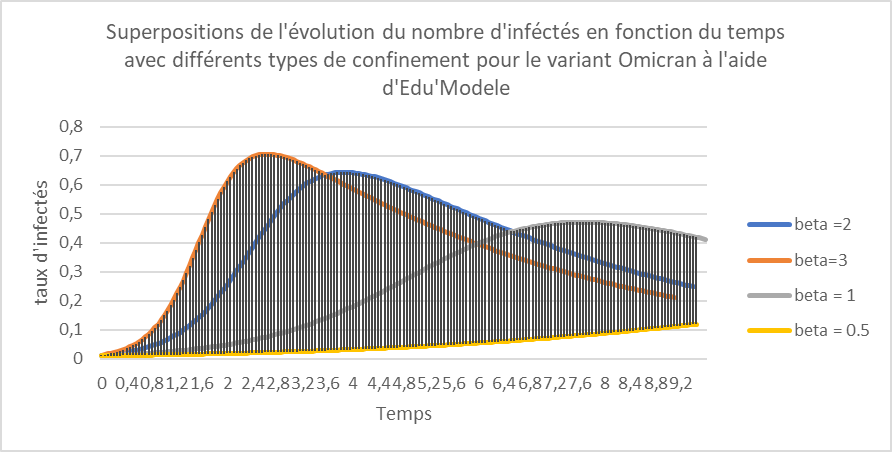
On cherche à justifier l’impact des règles de distanciation sociales dans la propagation de l’épidémie de COVID-19, avant de chercher à justifier l’intérêt de la vaccination.

NOTIONS, SAVOIR-FAIRE, compétences
Notions	Extrait du programme de Première Spécialité : Dans une population, cette vaccination n’offre une protection optimale qu’au-delà d’un certain taux de couverture vaccinale, qui bloque la circulation de l’agent infectieux au sein de cette population. Cela résulte du fait que l’on peut porter et transmettre l’agent infectieux sans être soi-même malade (porteur sain).
Capacités	Savoir expliciter ses comportements face à un risque de santé pour exercer sa responsabilité individuelle ou collective. - Modéliser et calculer le taux de couverture vaccinale efficace pour un vaccin (par exemple : vaccination contre la rougeole).

Cadre de référence des compétences numériques (CRCN)
	Programmer
	Évoluer dans un environnement numérique
	Gérer des données Traiter des données Programmer

Déroulement de la séquence

ACTIVITÉ
Durée : 1h – étape 1 : 20 minutes – étape 2 : 30 minutes – étape 2 : 5 minutes et temps de correction. Horaire total : 1 heure	Coût : 0 euros	Sécurité : RAS

Outils numériques et ressources
Édu’modèles analytique et sa fiche technique Modèle SIR d’une épidémie, à télécharger puis à charger dans Édu’modèles Modèle SIR Tableur et sa fiche technique

Handi-accessibilité
Pour les élèves malvoyants, adaptation du texte et utilisation d’un outil loupe. L’exploration de l’écran peut demander de laisser un peu de temps.

Un point de connaissances pour l’enseignant

De manière générale, un modèle est une simplification du réel dans laquelle on doit pouvoir changer des variables d’entrée et obtenir des valeurs en sortie.
Entre les deux, le modèle est construit pour reproduire un processus réel, qu’il s’agisse d’un modèle analogique ou d’un modèle numérique. Ce dernier passera par une mise en équations basée sur les connaissances acquises, complétées des éventuelles hypothèses nécessaires.
Le modèle doit ensuite être ajusté et validé par comparaison avec le réel, qu’il doit reproduire.
Il peut alors être exploité dans différents scénarios, avec des valeurs d’entrée correspondant à d’autres situations que celles observées.

La démarche de modélisation ne se limite donc pas à l’utilisation d’un modèle clé en main. Il faut donner à l’élève l’occasion de modifier le modèle, au moins dans ses paramètres, puis éventuellement de le compléter, voire de la construire. On a là une progressivité qui peut être mise en place au fil des séances.

Un modèle à compartiments est un modèle dans lequel on définit plusieurs réservoirs ainsi que les flux entre ces compartiments.
Ces modèles à compartiments sont présents depuis de nombreuses années en SVT, par exemple associés au logiciel Vensim pour le cycle de l’eau ou le cycle du carbone, comme proposé sur le site Access.
Toutefois le logiciel Vensim présente deux inconvénients (surmontables) :
- il nécessite une installation, ce qui le rend incompatible avec un usage sur les ordinateurs prêtés par la Région Île-de-France ;
- il n’est pas très intuitif et sa prise en main est difficile à justifier pour un usage ponctuel.
  C’est pourquoi on a choisi ici d’essayer de l’adapter dans Édu’modèles.

Construction du modèle

Dans le modèle SIR, on divise la population en trois catégories : Sain (S), Infectés (I) et Guéris (R).

On s’est ici appuyé sur la proposition de la page Modélisation d’une épidémie du site Images des mathématiques pour la transposer dans Édu’modèles.
Toutes les explications nécessaires y sont données. Dans ce modèle, il y a un premier flux du compartiment S vers le compartiment I, correspondant à l’infection de sujets sains, puis un flux du compartiment I vers le compartiment R, correspondant à la guérison.
Dans ce premier modèle simple, il n’y a pas de décès et on considère que les individus guéris sont immunisés (sinon il y aurait un flux de retour vers le compartiment S).
Le flux de S vers I dépend d’un taux de transmission à définir et de l’effectif des compartiments S et I.
Le flux de I vers R dépend d’un taux de guérison à définir et de l’effectif du compartiment I.

Dans Vensim, les compartiments mais aussi les flux peuvent être définis par une équation. Dans Édu’modèles, les relations seront ici définies dans l’équation de la variable.
Les taux de transmission et de guérison seront ici des variables distinctes, ce qui permettra de les manipuler directement.

Images des mathématiques nous propose le système suivant pour le modèle SIR :

**Les équations sur le site Images mathématiques**

Ce que nous transposerons en paramétrant le taux de variation (et non la valeur) de la manière suivante pour nos variables S, I et R :

S diminue du flux vers I, correspondant aux infections
d(S)/dt est décroissant (d’où le - ) et dépend du taux de transmission β correspondant à v[1], de sa propre valeur v[3] et du nombre d’infectés I donnée par v[4]

-βS(t)I(t) devient -v[1]*v[3]*v[4]

I augmente de ce qui vient de S et diminue de ce qui va vers R (ceux qui guérissent)
d(I)/dt dépend d’une part du taux de transmission v[1], de sa propre valeur v[3] et du nombre d’infectés I donnée par v[4], d’autre part du taux de guérison γ donné par v[2]

βS(t)I(t) - γI(t) devient (v[1]*v[3]-v[2])*v[4]

R augmente de ce qui vient de I
d(R)/dt est croissant et dépend du taux de guérison γ donné par v[2] et du nombre d’infectés I donnée par v[4]

Paramétrage

Vérification du modèle

Images mathématiques propose cet exemple de résultat :

**Un résultat avec le modèle sur la page Images mathématiques**

Avec un taux de transmission de 0,8, un taux de guérison de 0,05, et 50% d’infectés au départ, nous obtenons le résultat suivant avec notre modèle dans Édu’modèles :

(Nous partons ici du principe que le modèle proposé par Images mathématiques est valide et que nous cherchons juste à le transposer dans un autre logiciel.)

Déroulement détaillé

Activité : modèle SIR

Étape 1 : Découverte du modèle

Compréhension du modèle : un texte, reprenant les explications du site Images mathématiques, est fourni et pour obliger à regarder les formules, on demande d’identifier de quoi dépend le nombre d’infectés.
Adaptation du modèle la question faisant le lien avec la COVID-19, il faut adapter le taux de transmission et le le taux de guérison.
On demande de les calculer à partir des données fournies, puis de paramétrer le modèle.

La rougeole a un taux de reproduction de base (R0) entre 15 et 20 (une personne infectée peut contaminer jusqu’à 15 à 20 personnes non immunisées).
La forme initiale du SARS Cov2 avait un R0 proche de 2,5, le variant Alpha autour de 4, le variant Delta compris entre 6 et 8. Le variant Omicron pourrait avoir un R0 autour de 12 ou 15, proche de la rougeole, parmi les plus contagieux connus. On prendra β/γ =15.
On prendra 1/γ = 5 jours comme durée moyenne de contagion.

Étape 2 : utilisation du modèle pour justifier les mesures de distanciation sociale

Notre modèle de départ correspond à une propagation de l’épidémie sans mesure de limitation, nous allons l’adapter avec des scénarios de distanciation sociale plus ou moins poussée.
Pour cela on demande :

d’identifier le ou les paramètre(s) du modèle qui seraient influencés par une distanciation sociale (ici ce serait le taux de transmission)
de faire tourner le modèle en faisant varier la valeur de ce paramètre pour modéliser différents niveaux de confinement : ne rien faire, isolement des cas, isolement des cas + quarantaine des cas contacts, fermeture des écoles et des universités (les valeurs sont choisies de manière arbitraire.)

Les résultats sont exportés au format csv pour pouvoir être superposés.

Exemple de production élève

D’après notre modèle, les mesures de distanciation permettent d’étaler les contaminations, ce qu’il faudra relier à la capacité des hôpitaux à traiter les patients.

Images mathématiques propose ce résultat issu d’une étude au Royaume-Uni :

**Le résultat d’une étude avec une modélisation des lits occupés dans les hôpitaux en fonction des mesures prises**

On y voit un résultat assez similaire à celui obtenu en classe.

Étape 3 : Et la vaccination ?

Dans ce modèle, vacciner revient à créer un flux directement du compartiment S au compartiment R, sans passer par I.
On demande alors aux élèves de compléter le modèle, au moins sur papier, dans le logiciel pour les plus à l’aise.

NB : Par rapport au modèle multi-agents proposé dans cet article, on définirait plutôt un taux de vaccination pour créer un flux de S vers R. On ne définit donc pas un taux de vaccinés dans la population au départ, mais plutôt quel taux d’individus vont être vaccinés à chaque "tic".
La question ne serait donc pas « Quel pourcentage d’individus doivent être vaccinés pour empêcher la propagation du pathogène ? » mais plutôt « Quel pourcentage d’individus doivent être vaccinés chaque unité de temps pour empêcher la propagation du pathogène ? »

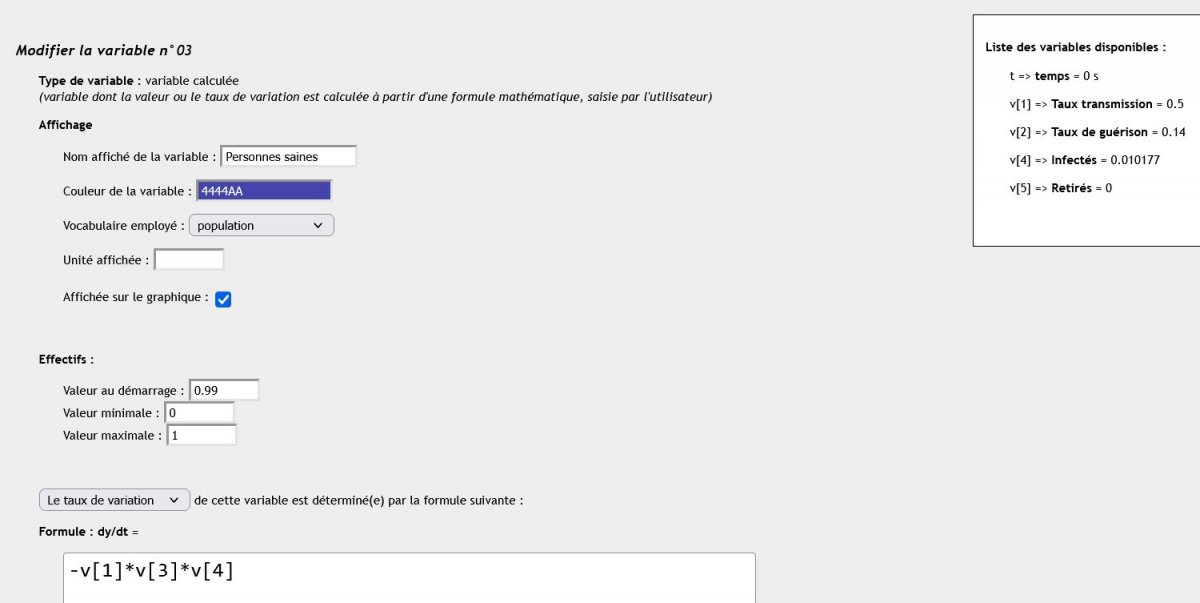
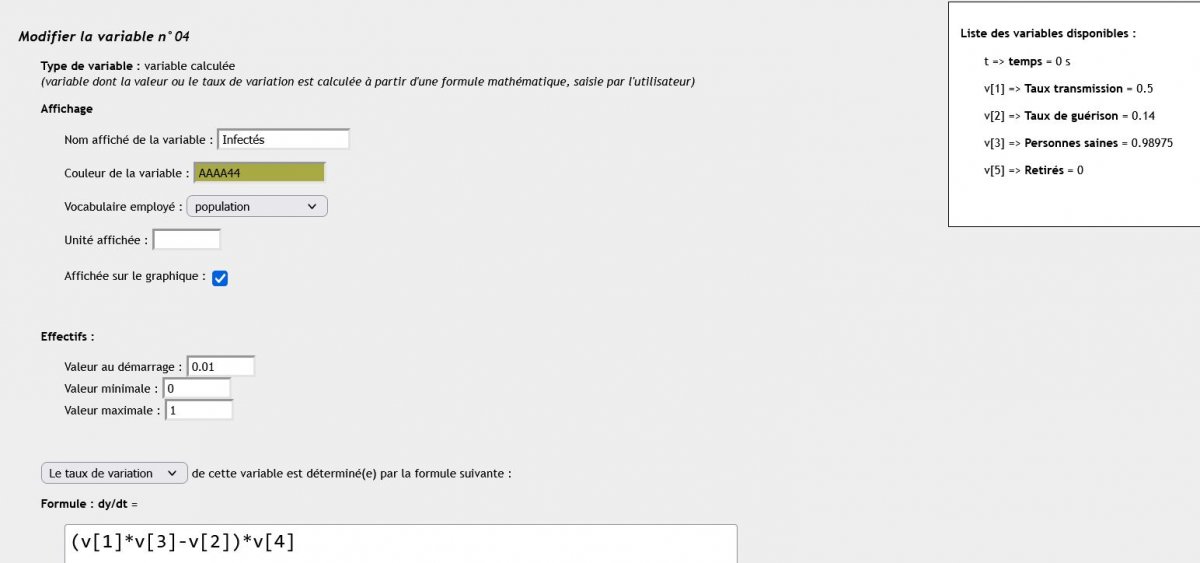
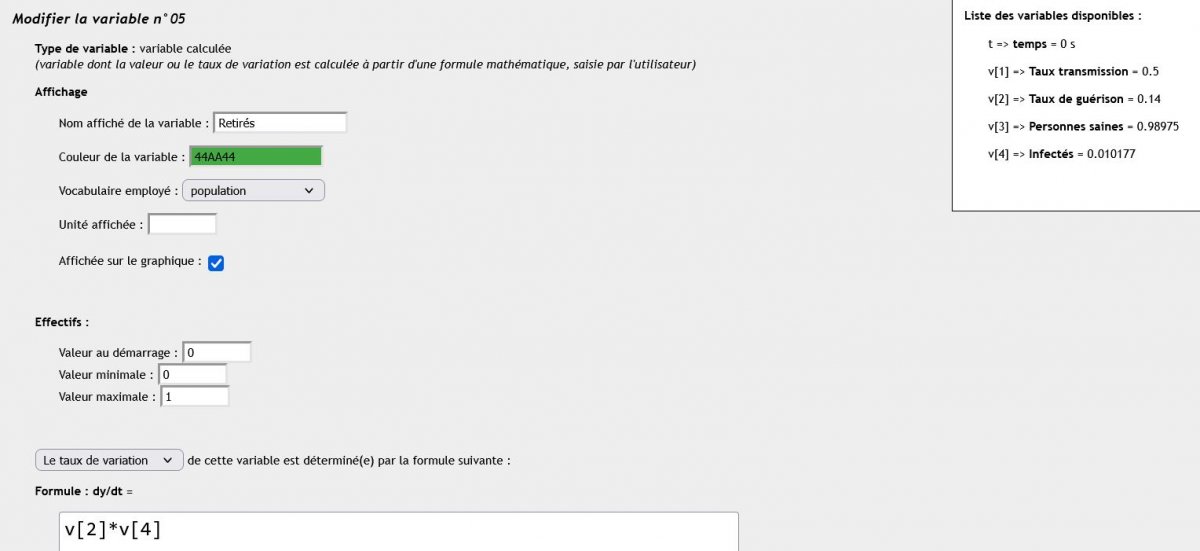
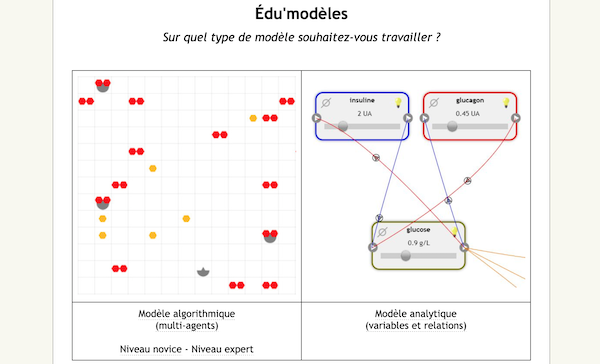
Focus sur un outil : Édu’modèles analytique

Le module analytique d’Édu’modèles permet de modéliser des variables et leurs relations.
Une variable peut être une grandeur quelconque, les relations correspondent à l’influence que leur valeur va avoir sur d’autres variables ou réciproquement.
Une fois le modèle lancé, les variables vont évoluer en fonction des règles qui ont été définies, spontanément et/ou sous l’influence des valeurs des autres variables.
Des curseurs permettent de modifier les valeurs pendant l’avancée du modèle.
Lire : Édu’modèles (module analytique), un logiciel pour modéliser en SVT.

Des exemples de modèles analytiques clé en main sont proposés à partir de l’accueil d’Édu’modèles.

Avantages / Plus-values

L’interface d’Édu’modèles est assez simple d’utilisation et permet facilement aux élèves de modifier les paramètres du modèle.

Points de vigilance

Si l’interface est assez simple, elle demande pour être bien exploitée d’avoir bien compris les paramètres du modèle sur lequel on travaille, afin de déterminer à quel endroit on doit agir.
Les modèles proposés en exemple dans Édu’modèles analytique sont plutôt des modèles associés à des TP de Terminale. Il y a peu d’exemples en Première. Il sera donc plus difficile de réinvestir l’outil avant la Terminale.

Analyse et pistes d’amélioration

ANALYSE ET ÉVALUATION DU DISPOSITIF
Plus-values dégagées	Le modèle SIR est relativement simple à comprendre, avec un nombre de compartiments et de flux assez restreint. Ce ne serait pas le cas dans un TP où on chercherait à reconstruire un cycle du carbone, comme proposé ici dans Vensim. Associé à Édu’modèles, le modèle SIR est relativement accessible et donc modifiable. Images mathématiques propose directement des simulations interactives qui permettent d’arriver au même résultat. Il est toutefois plus formateur de pouvoir voir ce qu’il y a derrière la simulation, ce qu’il se passe entre le curseur que l’on déplace et le résultat qui s’affiche. Positionner la vaccination dans le modèle SIR en donne une vision différente (passage du compartiment S au compartiment R) et claire et permet de bien en montrer l’intérêt.
Difficultés rencontrées	L’aspect mathématique peut rebuter et décourager certains élèves, en particulier ceux qui ne suivent pas de Spécialité Mathématique. Concrètement le passage "si β/γ =15 et 1/γ = 5 alors combien vaut β ?" a été une difficulté et rend nécessaire un accompagnement en fonction des profils.

ANALYSE ET ÉVALUATION DU DISPOSITIF

Plus-values dégagées

Le modèle SIR est relativement simple à comprendre, avec un nombre de compartiments et de flux assez restreint.
Ce ne serait pas le cas dans un TP où on chercherait à reconstruire un cycle du carbone, comme proposé ici dans Vensim.
Associé à Édu’modèles, le modèle SIR est relativement accessible et donc modifiable.
Images mathématiques propose directement des simulations interactives qui permettent d’arriver au même résultat. Il est toutefois plus formateur de pouvoir voir ce qu’il y a derrière la simulation, ce qu’il se passe entre le curseur que l’on déplace et le résultat qui s’affiche.
Positionner la vaccination dans le modèle SIR en donne une vision différente (passage du compartiment S au compartiment R) et claire et permet de bien en montrer l’intérêt.

Difficultés rencontrées

L’aspect mathématique peut rebuter et décourager certains élèves, en particulier ceux qui ne suivent pas de Spécialité Mathématique.
Concrètement le passage "si β/γ =15 et 1/γ = 5 alors combien vaut β ?" a été une difficulté et rend nécessaire un accompagnement en fonction des profils.

Voir en ligne : Édu’modèles analytique

Galerie d'images

Des modèles en démo dans le module analytique

Agenda

Voir tout l'agenda

Dans la même rubrique

Quelques exemples de situations de formation aux capacités expérimentales adaptées au programme de 1ère spécialité SVT pour découvrir l’épreuve pratique

Un échantillon de situations d'évaluation des compétences expérimentales pour une utilisation parcimonieuse avec des élèves de première en spécialité SVT.

Présenter l’ECE aux élèves de Première

16 mars 2026

Modéliser l’évolution des résistances en lien avec les pratiques humaines

Étudier grâce à la modélisation numérique, l’effet des pratiques humaines sur la sélection des résistances aux antibiotiques chez les bactéries et aux insecticides chez les insectes ravageurs des cultures.

12 novembre 2025

Haro sur le Bouquetin des Alpes

Dans cette histoire dont vous êtes le héros sur support numérique, les élèves mènent l'enquête pour comprendre les stratégies biosécuritaires dans les élevages, réfléchissent à l'adéquation de leur application aux populations sauvages, et travaillent sur les barres d'erreur et les intervalles de confiance.

Terminale Enseignement scientifique

2 juillet 2025