| - Liaison avec le programme et place dans la progression
– Problème à résoudre – Notions, savoir-faire, compétences – Outils numériques et ressources – Déroulement de la séquence |

|
Professeur
- Anne FLORIMOND, lycée Richelieu à Rueil-Malmaison (92)
| LIAISON AVEC LE PROGRAMME | |
|---|---|
| Niveau concerné | Terminale spécialité SVT |
| Partie du programme : | À l’intérieur du thème « Génétique et évolution », dans le sous-thème : « L’inéluctable évolution des génomes au sein des populations ». |
| PLACE DANS LA PROGRESSION |
|---|
| Après avoir vu, dans le sous-thème « Le brassage des génomes à chaque génération : la reproduction sexuée des eucaryotes », les notions :
– chaque cellule produite par méiose reçoit un seul des deux allèles de chaque gène avec une probabilité équivalente ; – les gamètes se rencontrent au hasard lors de la fécondation |
| MOTIVATION |
|---|
| S’impliquer dans la modélisation numérique et la programmation. Ne pas utiliser un modèle tout fait qui soit une boite noire. Comprendre une loi théorique en l’exprimant avec un algorithme sans avoir à écrire de code. Utiliser un logiciel avancé, c’est-à dire "qui permet à l’utilisateur de faire ses propres simulations sans être pour autant informaticien". |
| PROBLEME A RESOUDRE |
|---|
| « On veut montrer que les connaissances sur la reproduction sexuée corroborent la prédiction du modèle théorique de Hardy-Weinberg, en construisant un modèle numérique de suivi de deux allèles d’un gène dans une population. » |
| NOTIONS, SAVOIR-FAIRE, COMPETENCES | |
|---|---|
| Notions | Extraits du Bulletin officiel spécial n°8 du 25 juillet 2019 Dans les populations eucaryotes à reproduction sexuée, le modèle théorique de Hardy-Weinberg prévoit la stabilité des fréquences relatives des allèles dans une population. Mais, dans les populations réelles, différents facteurs empêchent d’atteindre cet équilibre théorique : l’existence de mutations, le caractère favorable ou défavorable de celles-ci, la taille limitée d’une population (effets de la dérive génétique), les migrations et les préférences sexuelles. |
| Savoir-faire | Sélectionner des informations à partir du réel ou de documents. Travailler en équipe. Prendre en compte les avis d’autrui. Communiquer dans un langage scientifiquement approprié : oral, écrit, graphique, numérique. |
| Compétences | Concevoir, créer, réaliser. Communiquer et utiliser le numérique |
| Cadre de référence des compétences numériques (CRCN) | |
|---|---|
| Communication et collaboration |
|
| Création de contenus |
|
| Informations et données |
|
| ACTIVITE | ||
|---|---|---|
| Durée : 1h (modélisation seule) ou 2h (modélisation suivie de l’investigation de situations d’écart par rapport à l’équilibre théorique) | Coût : O euros | Sécurité : RAS |
| Outils numériques et ressources |
|---|
NetBioDyn est un logiciel de modélisation multi-agents créé par le mathématicien Pascal Ballet en 2007 à destination des élèves du secondaire et des étudiants du supérieur, de la L1 au master 2. Convivial et intuitif, il permet de créer des modèles sans avoir de code à écrire. NetBioDyn a fini par inspirer la conception d’un autre logiciel, Edu’Modèles (auteur : Philippe Cosentino) qui en a repris les grands principes.
|
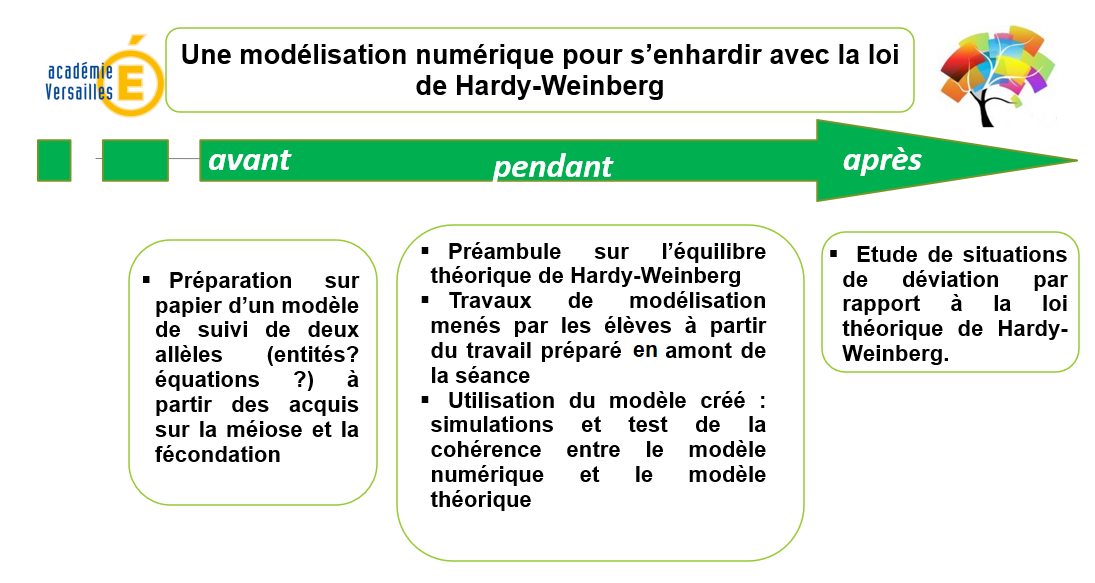
Déroulement global de la séquence
Déroulement détaillé de la séquence
1. Avant la modélisation numérique
Quel que soit l’itinéraire (avec ou sans création complète du modèle numérique) proposé aux élèves, il est toujours utile de préparer « sur papier » la modélisation. Ce travail préparatoire peut être fait par les élèves avant la séance, en leur donnant les consignes suivantes :
▪ On considère, dans une population, un gène représenté par deux allèles (notés A1 et A2).
▪ Il faut prévoir les entités à déclarer dans le modèle. Il s’agit ici des différentes sortes de génotypes donc de combinaisons des deux allèles.
▪ Pour calculer l’évolution au cours du temps des effectifs des génotypes des différents individus, le modèle doit comporter des équations matérialisant toutes les possibilités de reproduction entre les individus. Il doit aussi tenir compte des proportions des descendants obtenus.
Un tableau (à ne pas confondre avec un échiquier de croisement) permet de préparer la modélisation. Pour le bâtir, on peut conseiller aux élève de procéder de la manière suivante :
– indiquer en ligne et en colonne les génotypes possibles pour les deux géniteurs ;
– rayer les cases redondantes ;
– noter à l’intersection ligne/colonne les génotypes des descendants obtenus (pour chaque reproduction, se limiter à l’obtention de 4 individus en respectant leurs proportions))]
Une fois le tableau rempli, on a finalement les équations qu’il faudra déclarer au moment de la construction du modèle numérique, car chaque case du tableau donne, comme l’aurait fait un échiquier de croisement, le résultat statistique de la rencontre entre deux entités.
Télécharger ces consignes sous la forme d’un document de travail pour les élèves :
Télécharger le tableau déjà rempli :
2. Autour des formulations de l’équilibre théorique de Hardy-Weinberg
En 1908, Hardy et Weinberg proposent un modèle théorique qui prévoit, sous certaines conditions, la stabilité des fréquences relatives des allèles dans les populations eucaryotes à reproduction sexuée.
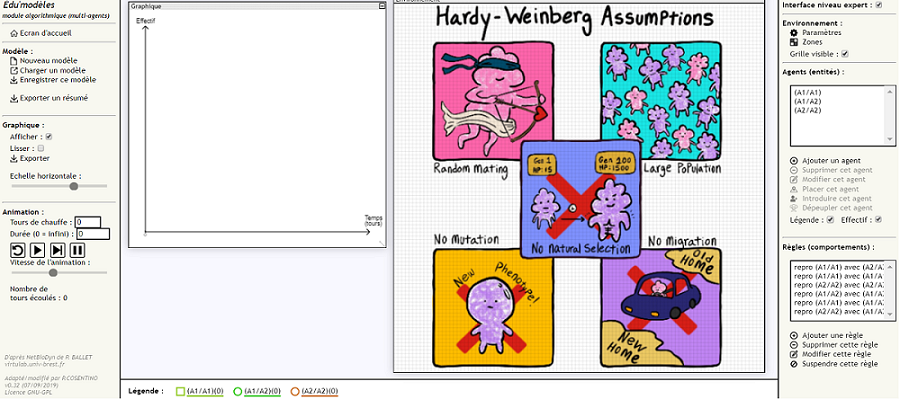
Cette affiche réalisée par les soeurs amibes ("AmeobaSisters")1 décline les hypothèses ("assumptions" ) que nécessite l’équilibre de Hardy-Weinberg. Le décryptage des conditions de l’équilibre peut être fait avec les élèves :
- No selection : la population n’est pas soumise à la sélection naturelle
- No mutation : aucun nouvel allèle n’apparaît dans la population par modification d’un allèle préexistant
- No migration : la population n’est pas extraite d’un échantillon d’une population initiale
- Large population : la population n’est pas soumise à la dérive génétique
- Random meetic : les couples se forment au hasard
1Les deux auteures démystifient la science en créant, toujours avec humour, des vidéos gratuites, images, documents, ressources et bandes dessinées.
3. La création du modèle numérique
Les élèves n’ayant pas tous la même appétence pour l’algorithmique, on pourra proposer différents itinéraires :
- Itinéraire 1 : Créer intégralement le modèle
- Itinéraire 2 : Finaliser un modèle incomplet
- Itinéraire 3 : Justifier l’algorithme d’un modèle opérationnel
– Dans un modèle, chaque entité est définie par sa mobilité et sa demi-vie. La demi-vie d’une entité est la durée au bout de laquelle la moitié de la population de cette entité a disparu.
– Les unités de temps, exprimant les durées, sont arbitraires. On parlera de "tics" sous NetBioDyn et de "tours" sous Edu’Modèles.
– Une équation de comportement s’écrit comme une réaction chimique : les réactifs en amont et les produits en aval.
– Pour éviter l’encombrement rapide de l’environnement par de trop nombreux agents :
- paramétrer un environnement de 100 x 100 soit 10000 pixels
- ne pas donner une probabilité trop forte aux comportement de reproduction : éviter les valeurs supérieures à 0,1 dans le cas de NetBioDyn ou supérieures à 10% dans le cas d’Edu’Modèles
– Lors des simulations, laisser un écoulement de temps suffisamment long pour simuler une durée représentative de plusieurs générations.
Détaillons les itinéraires :
Itinéraire 1 : la création intégrale du modèle
Des tutoriels sont disponibles pour la construction d’un modèle avec Edu’Modèles ou avec NetBioDyn.
Si NetBiodyn est choisi, les six entités à déclarer le seront au moyen du bouton entités :
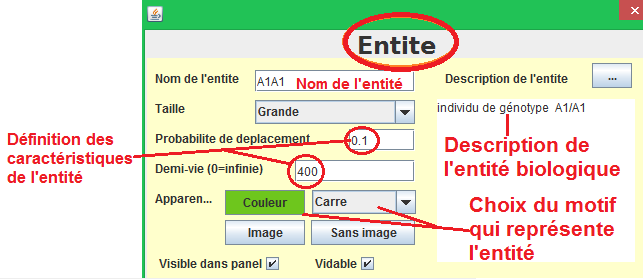
Le bouton comportements permet de déclarer une par une les équations trouvées lors du travail préparatoire :
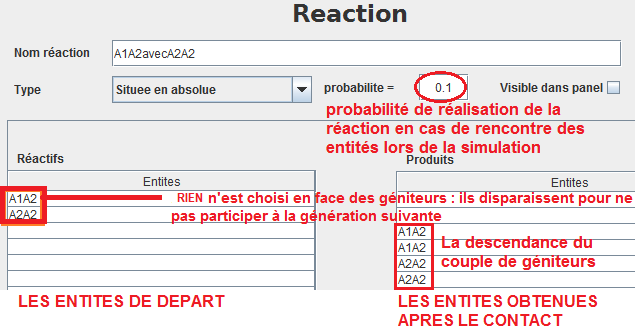
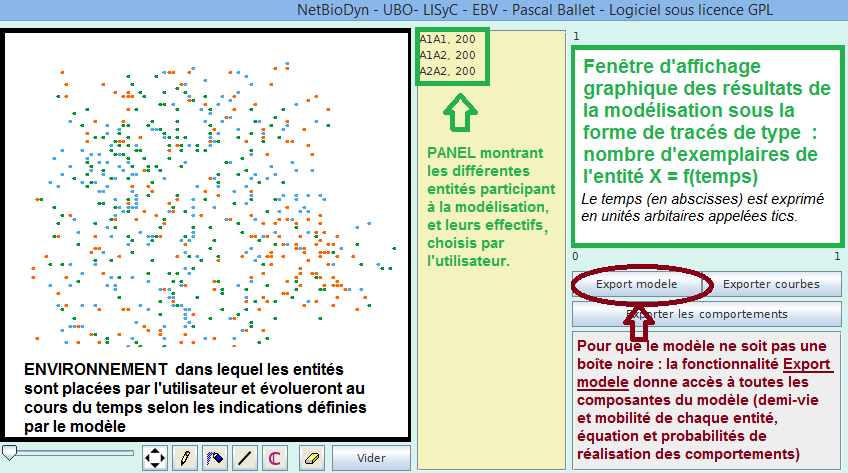
Le bouton Export modele permet, à tout moment de la construction du modèle, d’en visualiser un résumé (ci-dessous, le décodage d’un comportement) :

Une fois le modèle créé, prévoir un dossier d’enregistrement. Ce dernier contiendra, après l’enregistrement, un fichier dont l’extension est .nbd (c’est-à-dire le modèle lui même) ainsi que d’autres fichiers utiles (à ne pas supprimer, sauf ceux dont la taille est de 0 Ko)
Itinéraire 2 : la finalisation d’un modèle incomplet
Télécharger le modèle incomplet :
Voir le résumé du modèle incomplet :

Les élèves auront donc à rajouter trois équations manquantes. Ils pourront s’appuyer sur le travail préparatoire pour compléter leur modèle.
Itinéraire 3 : la justification de l’algorithme d’un modèle opérationnel
Les élèves qui ont choisi cet itinéraire ont droit au modèle complet (avec un décor d’environnement évocateur du sujet, pour motiver les troupes !)
Télécharger le modèle complet :
Voir le résumé du modèle complet :

Il est attendu que les élèves puissent justifier les propriétés des entités et des comportements à l’aide du travail préparatoire et des contraintes connues de l’équilibre théorique de Hardy-Weinberg.
Voici un exemple de raisonnement :
| Particularité du modèle | Justification |
|---|---|
| Tous les agents ont la même demi-vie | La population n’est pas soumise à la sélection naturelle |
| Tous les agents ont la même mobilité | Les couples se forment au hasard |
| Tous les couples ont le même nombre de descendants à chaque rencontre | La population n’est pas soumise à la sélection naturelle |
| Tous les couples ont la même probabilité d’avoir des descendants | La population n’est pas soumise à la sélection naturelle |
4. Le test du modèle numérique et sa confrontation au modèle théorique
Tous les élèves, quel que soit l’itinéraire choisi, sont dotés de leur modèle. Il s’agit désormais de le faire fonctionner.
L’écran ci-dessous illustre le principe d’une simulation avec un modèle multi-agents, par exemple NetBioDyn (voir ce tutorielpour faire tourner un modèle) :
Les effectifs des différents génotypes, calculés par le modèle à tout moment de la simulation, peuvent ensuite être traités avec un tableur afin d’obtenir les fréquences alléliques :
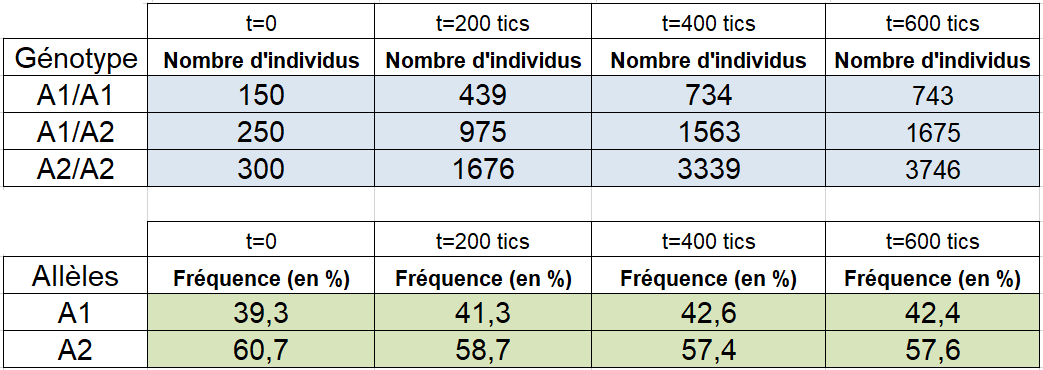
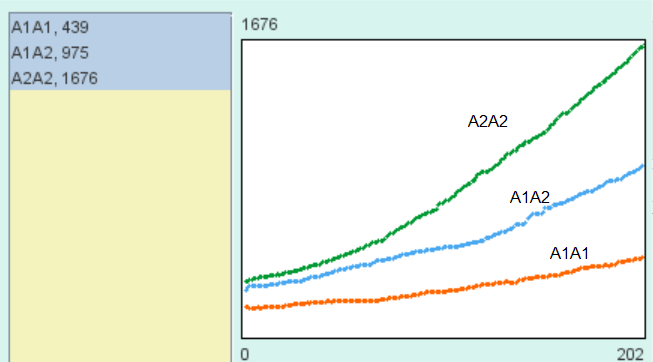
Voici des exemples de résultats bruts obtenus avec NetBioDyn, relevés tous les 200 tics :
| Effectifs à t=0 | Graphique de l’évolution des effectifs jusqu’à t=200 tics | Graphique de l’évolution des effectifs jusqu’à t=400 tics | Graphique de l’évolution des effectifs jusqu’à t=600 tics |
|---|---|---|---|

|
|
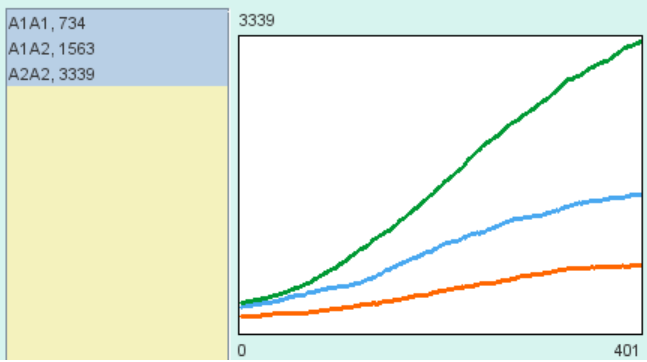
|
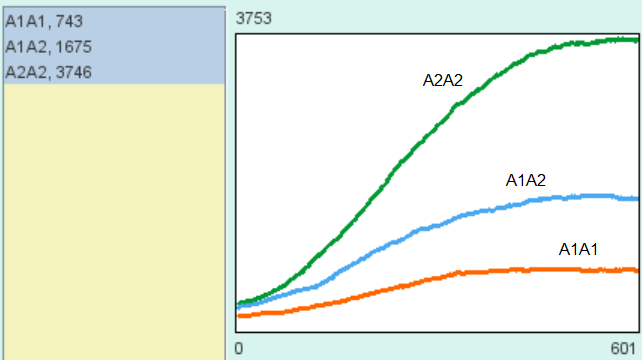
|
Le calcul des fréquences alléliques à partir des effectifs des génotypes donne les résultats suivants :
Les utilisateurs d’Edu’Modèles pourront même enregistrer les valeurs du graphique sous la forme d’un fichier CSV puis les traiter avec un tableur-grapheur pour le calcul des fréquences alléliques. On obtiendra alors ce type de graphique, qui témoigne très bien de la stabilité des fréquences alléliques :
Il s’agit bien de la prédiction du modèle théorique de Hardy-Weinberg.
5. Les prolongements possibles de la séance
Concrètement, bien plus que de redémontrer l’équilibre théorique de Hardy-Weinberg, le programme de spécialité SVT propose surtout d’étudier les facteurs empêchant d’atteindre l’équilibre théorique.
On pourra donc mettre à profit le modèle confectionné pour interpréter des situations de "non-respect" des conditions fixées par Hardy et Weinberg. Ce travail se prêterait bien à des ateliers. Voici quelques suggestions :
Atelier 1 : Des élèves déçus
À l’aide de simulations appropriées, expliquer aux élèves leur déconvenue.
Atelier 2 : Étonnantes drosophiles
Modifier le modèle numérique pour qu’il rende compte de l’évolution observée par les étudiants.
Atelier 3 : Chez les Dunkers
À l’aide de simulations appropriées, expliquer la particularité de la population de Dunkers.
On aura ainsi mis en évidence trois situations d’écart entre les fréquences alléliques réelles et celles prédites par le modèle théorique de Hardy-Weinberg : la dérive génétique et son importance dans le cas d’une population de petite taille (atelier 1), le caractère favorable ou défavorable d’une mutation (atelier 2) et les migrations (atelier 3).
Une approche multi-agent pour la simulation en biologie cellulaire
Auteur de cet article : Anne FLORIMOND, professeur de SVT au lycée Richelieu (Rueil-Malmaison), professeur formateur co-animant avec Isabelle Digard les formations hybrides "Recourir aux modèles en SVT au lycée" et "Utiliser des bases de données scientifiques en TP" (PAF académie de Versailles), professeur associé aux travaux de recherche de l’Institut Français de l’Education (équipe Acces, groupe "Microbes, immunité et vaccination") et membre du GEP Versailles.