Avertissement : ce n’est pas une séquence pédagogique qui est proposée ici, mais une explication détaillant la manière de présenter une simulation du modèle de Hardy-Weinberg sous la forme d’un algorithme. Il est souhaitable d’avoir quelques bases en algorithmique et en Python pour pouvoir comprendre les programmes présentés.
Professeur
- Stanislas Dorey - Lycée Albert Camus Bois Colombes
| LIAISON AVEC LE PROGRAMME | |
|---|---|
| Niveau concerné | Terminale : enseignement scientifique |
| Partie du programme : | Une histoire du vivant La biodiversité et son évolution |
| PLACE DANS LA PROGRESSION |
|---|
| Dans le thème 3 "Une histoire du vivant", dans le point "La biodiversité et son évolution", il est demandé de produire un programme en Python pour prouver ou constater que les probabilités des génotypes sont constantes à partir de la seconde génération (modèle de Hardy-Weinberg). |
| Cadre de référence des compétences numériques (CRCN) | |
|---|---|
| Communication et collaboration |
|
| Création de contenus |
|
| Environnement numérique |
|
| Informations et données |
|
| NOTIONS, SAVOIR-FAIRE, COMPETENCES | |
|---|---|
| NOTIONS | Extraits du Bulletin officiel spécial n°8 du 5 juillet 2019 Au cours de l’évolution biologique, la composition génétique des populations d’une espèce change de génération en génération. Le modèle mathématique de Hardy-Weinberg utilise la théorie des probabilités pour décrire le phénomène aléatoire de transmission des allèles dans une population. En assimilant les probabilités à des fréquences pour des effectifs de grande taille (loi des grands nombres), le modèle prédit que la structure génétique d’une population de grand effectif est stable d’une génération à l’autre sous certaines conditions (absence de migration, de mutation et de sélection). Cette stabilité théorique est connue sous le nom d’équilibre de Hardy-Weinberg. |
| SAVOIR-FAIRE | Pour la transmission de deux allèles dans le cadre du modèle de Hardy-Weinberg, établir les relations entre les probabilités des génotypes d’une génération et celles de la génération précédente. Produire une démonstration mathématique ou un calcul sur tableur ou un programme en Python pour prouver ou constater que les probabilités des génotypes sont constantes à partir de la seconde génération (modèle de Hardy-Weinberg). Utiliser des logiciels de simulation basés sur ce modèle mathématique. |
| COMPETENCES |
|
| Outils numériques et ressources |
|---|
| Si on souhaite faire fonctionner le programme Python, il faut un environnement pour faire fonctionner Python. 3 solutions sont envisageables :
|
Proposition d’un algorithme pour simuler le modèle de Hardy-Weinberg
Pour étudier le modèle de Hardy-Weinberg, il faut s’intéresser à l’évolution de la fréquence des allèles d’un gène au fil des générations.
Pour cela, on part d’une population de départ P1 et l’on s’intéresse à un gène avec 2 allèles A et a où p est la fréquence de l’allèle A et q la fréquence de l’allèle a.
On va alors générer une population P2 issue de la reproduction d’individus de la population P1. On suppose que la taille de la population reste constante au fil des générations.
Pour générer un individu de P2, on tire au sort l’allèle porté par le gamète 1 en respectant les fréquences p et q. On fait de même pour le gamète 2. Enfin, on fusionne ces 2 gamètes pour obtenir le zygote.
Il suffit maintenant de répéter ces 3 opérations dans une boucle autant de fois qu’il y a d’individus dans la population P2.
A la fin de la boucle, on peut déterminer les nouvelles fréquences des allèles A et a dans la population 2 et les afficher. Ci-dessous, un exemple d’algorithme pour simuler la population P2.

Si on veut suivre l’évolution de p et q sur plusieurs générations, il suffit de répéter l’algorithme précédent autant de fois que l’on souhaite de générations. Pour cela, il faut inclure les opérations précédentes dans une boucle comme détaillé dans l’exemple ci-dessous.
Proposition d’un programme en Python pour simuler le modèle de Hardy-Weinberg
Il est possible de programmer en Python l’algorithme précédent. Voici quelques exemples de résultats qu’il est possible d’obtenir avec ce programme (à noter qu’il est tout à fait possible de se servir de ce programme sans comprendre son fonctionnement).
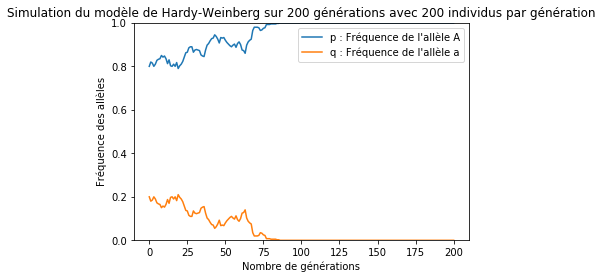
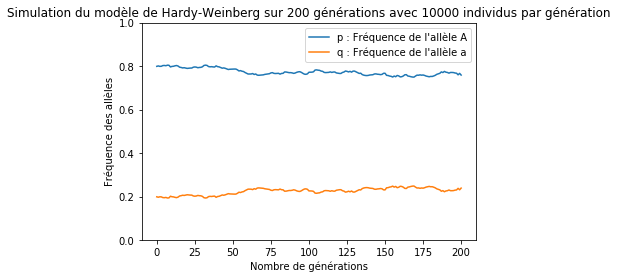
Afin de pouvoir bien comprendre le code proposé ici, il serait préférable de connaitre les notions suivantes en Python :
- les types de données int, float, string et list,
- la structure conditionnelle if et elif,
- la boucle while et la boucle for
- les fonctions print(), len() et input()
- (la librairie matplolib pour la présentation des résultats sous forme graphique)
Il aurait été possible de programmer cet algorithme de manière plus élégante, mais cela aurait été plus technique (utilisation de fonctions par exemple).
Le programme ci-dessous peut s’ouvrir dans n’importe quel éditeur de texte. Pour le faire fonctionner voir la section Outils numériques et ressources.
Lecture commentée du programme (mettre en plein écran) :

